在当今数字化时代,数据的处理和分析变得日益重要,图数据库作为一种强大的工具,正逐渐受到广泛关注,Neo4j 作为一款优秀的图数据库,其最短路径算法的创新更是为解决复杂的实际问题提供了有力支持。
最短路径算法是图论中的一个关键问题,它在众多领域都有着广泛的应用,如交通网络规划、社交网络分析、物流配送优化等,传统的最短路径算法在处理大规模图数据时,往往面临着效率低下、资源消耗大等挑战,而 Neo4j 所采用的最短路径算法则通过一系列创新手段,有效地克服了这些难题。
Neo4j 最短路径算法的创新之一在于其对图数据结构的优化,它采用了高效的存储方式和索引机制,能够快速定位节点和边,从而大大提高了算法的执行速度,Neo4j 还引入了并行计算的思想,充分利用多核处理器的优势,将计算任务分配到多个核心上同时进行,进一步缩短了计算时间。
另一个创新之处在于算法的智能选择策略,Neo4j 能够根据图的特点和用户的需求,自动选择最合适的最短路径算法,对于稀疏图,它可能会采用迪杰斯特拉算法;而对于稠密图,则可能会选择 A*算法或其他更高效的算法,这种自适应的算法选择机制,使得 Neo4j 在处理各种类型的图时都能表现出出色的性能。
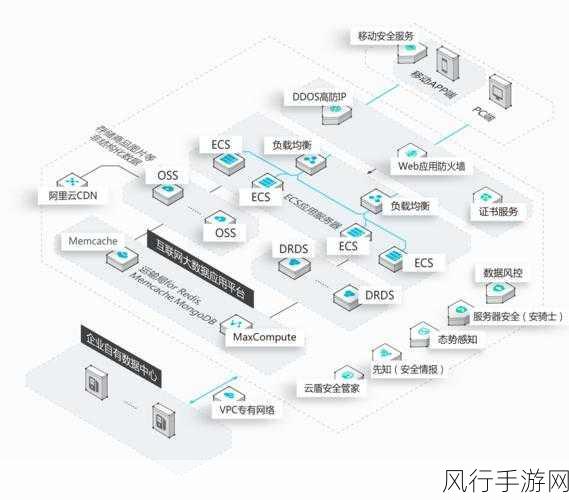
Neo4j 还注重与其他技术的融合与集成,它可以与机器学习算法相结合,通过对图数据的分析和挖掘,为最短路径的计算提供更准确的预测和指导,与大数据处理框架的集成,也使得 Neo4j 能够处理海量的图数据,拓展了其应用场景和范围。
为了更好地理解 Neo4j 最短路径算法的创新,我们可以通过一个实际案例来进行分析,假设我们要构建一个城市交通网络的图模型,其中节点代表各个路口,边代表道路,每条边都有相应的权重表示道路的长度或通行时间,使用 Neo4j 的最短路径算法,我们可以快速计算出从起点到终点的最优路径,帮助交通管理部门进行路线规划和拥堵疏导。
在未来的发展中,Neo4j 最短路径算法的创新仍将继续,随着技术的不断进步和应用需求的不断增长,我们可以期待它在算法效率、准确性、适应性等方面取得更大的突破,也希望它能够与更多新兴技术相结合,为解决各种复杂的现实问题提供更强大的支持和解决方案。
Neo4j 最短路径算法的创新为图数据库领域带来了新的活力和可能性,通过不断的探索和创新,相信它将在未来发挥更加重要的作用,为我们的生活和工作带来更多的便利和价值。