掌握递归函数编写的关键技巧

递归函数是编程领域中一种强大而富有魅力的工具，它能够以简洁而优雅的方式解决许多复杂的问题，但对于初学者来说，理解和编写递归函数可能会带来一些挑战。

递归函数的核心思想是函数自身调用自身，要成功编写递归函数，需要清晰地定义一个基本情况，也就是递归终止的条件，这个基本情况至关重要，否则递归可能会陷入无限循环，导致程序崩溃。

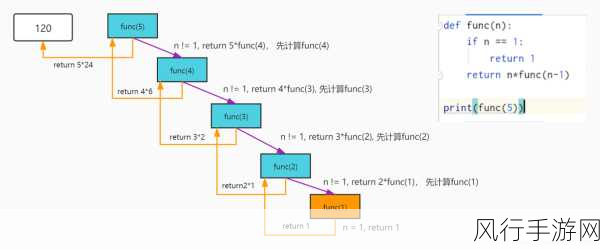
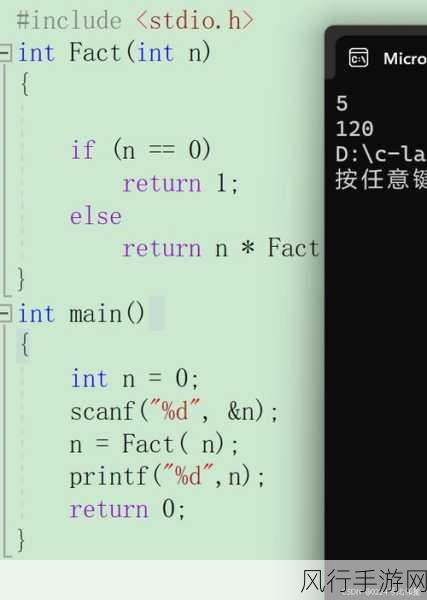
以计算阶乘为例，阶乘的定义是 n 的阶乘等于 n 乘以 (n - 1) 的阶乘，直到 n 为 1 时，阶乘为 1 ，我们可以这样编写一个计算阶乘的递归函数：

def factorial(n):
    if n == 1:
        return 1
    else:
        return n * factorial(n - 1)

在这个函数中，当 n 等于 1 时，就是基本情况，函数直接返回 1 ，否则，函数会通过自身调用计算 (n - 1) 的阶乘，并将结果乘以 n 。

再比如，计算斐波那契数列，斐波那契数列的定义是前两个数为 0 和 1 ，从第三个数开始，每个数都是前两个数之和，以下是用递归函数实现计算斐波那契数列的第 n 个数：

def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

这里，当 n 小于等于 1 时为基本情况，分别返回 0 和 1 ，否则，通过递归调用计算前两个位置的斐波那契数，并将它们相加。

编写递归函数时，要特别注意函数的逻辑是否清晰，是否能够正确处理各种边界情况，由于递归函数可能会导致大量的函数调用，对于一些大规模的计算，可能会出现性能问题，在实际应用中，需要根据具体情况权衡是否使用递归。

掌握递归函数的编写需要不断地练习和思考，深入理解其原理和应用场景，才能在编程中灵活运用，解决各种复杂的问题。